Chord
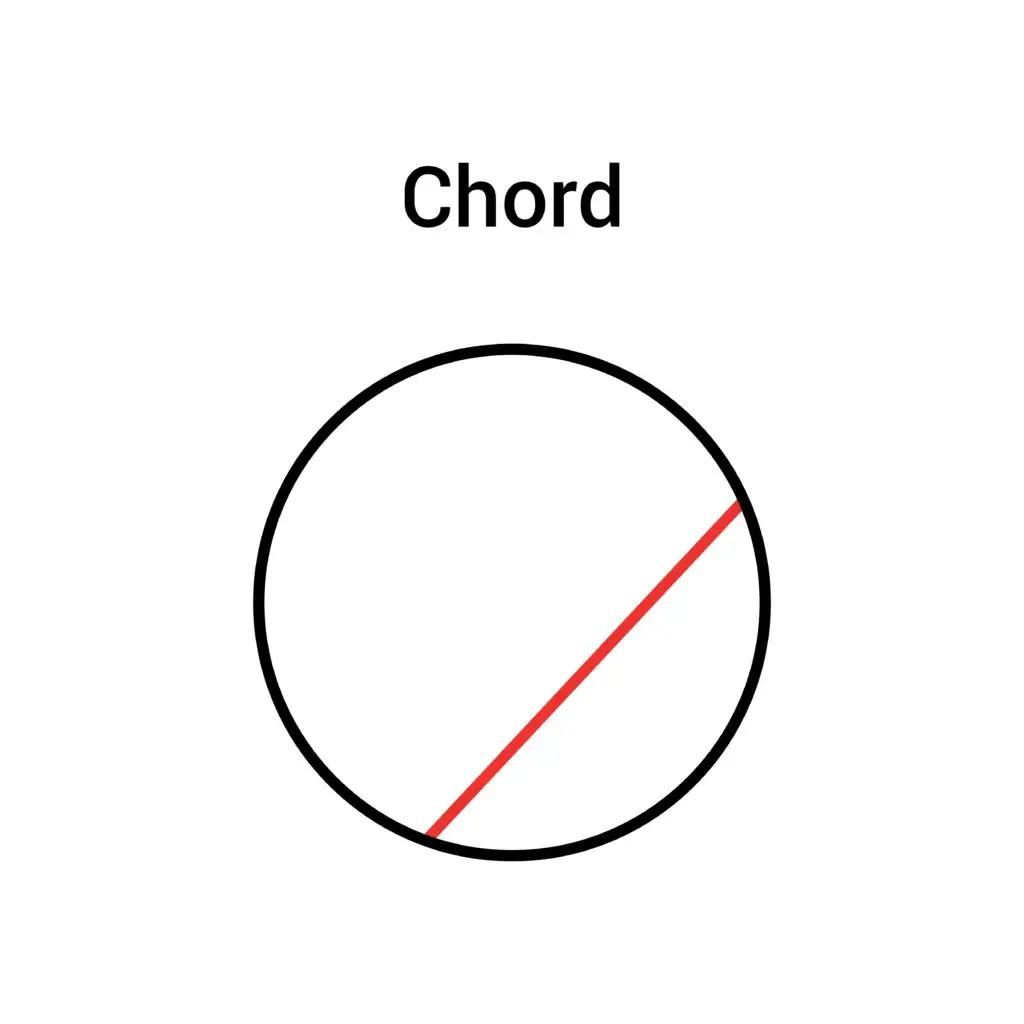
What is a Chord in Geometry?
A chord in geometry is a straight line segment that connects two points on the circumference of a circle. The longest chord in a circle is the diameter.
Chord in a Circle
A chord is a straight line that connects two points on the edge of a circle. It doesn’t have to go through the center of the circle, but it must stay inside the circle. For example, if you pick two points on the edge of a pizza and connect them with a line, that line is a chord.
The longest chord in a circle is called the diameter. The diameter passes through the center of the circle, dividing it into two equal halves. All other chords are shorter than the diameter because they don’t pass through the center.
Chords are important because they help us understand parts of a circle, like segments and arcs. For example, if you draw a chord, it divides the circle into two curved parts called arcs. The chord also creates a smaller section inside the circle, which is called a segment.
Chord Length Formula
The chord length formula helps you find the distance between two points on a circle’s edge. To use the formula, you need the radius of the circle and the perpendicular distance from the center of the circle to the chord.
The formula is:
![]()
Here:
 is the radius of the circle.
is the radius of the circle.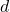 is the perpendicular distance from the center of the circle to the chord.
is the perpendicular distance from the center of the circle to the chord.
How It Works
- Start by finding the radius,
 , which is the distance from the center of the circle to its edge.
, which is the distance from the center of the circle to its edge. - Then, measure the perpendicular distance,
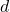 , from the center of the circle to the chord.
, from the center of the circle to the chord. - Substitute the values for
 and
and 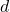 into the formula.
into the formula. - First, calculate
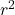 and
and 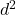 . Subtract
. Subtract 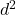 from
from 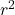 .
. - Take the square root of the result and multiply it by 2 to get the chord length.
Example
If the radius of the circle is ![]() and the perpendicular distance from the center to the chord is
and the perpendicular distance from the center to the chord is ![]() , find the chord length.
, find the chord length.
- Write the formula:
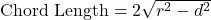
- Substitute
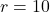 and
and 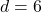 :
: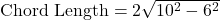
- Calculate
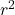 and
and 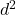 :
: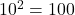 and
and 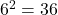
- Subtract:
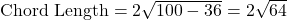
- Take the square root:
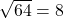
- Multiply by 2:
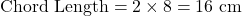
Final Answer
The chord length is ![]() .
.