Point

Definition of a Point

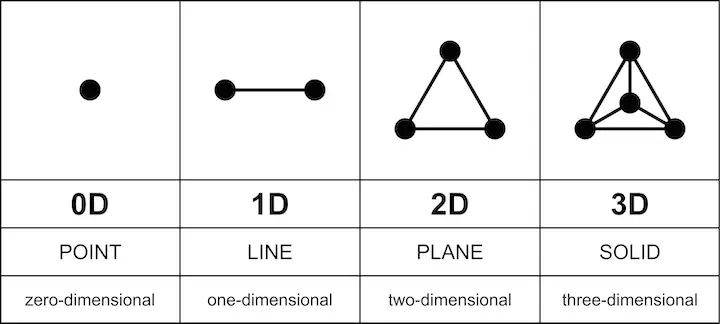
In geometry, a point is an exact location in space with no size, dimension, or length. It is often represented by a dot and serves as the basic building block for geometric figures.

Collinear & Coplanar Points

Collinear and coplanar points are two important ideas in geometry that describe how points are positioned. Collinear points are points that lie on the same straight line. For example, if you have three points—A, B, and C—and they all form a straight line, those points are collinear. If one point is not on the line, then the points are not collinear.

On the other hand, coplanar points are points that lie on the same flat surface, or plane. Imagine a sheet of paper with several dots drawn on it. As long as all the dots are on the paper, they are coplanar. However, if one dot is above or below the paper, then the points are not coplanar anymore.

The difference between the two is simple. Collinear points are about being on the same line, while coplanar points are about being on the same flat surface. All collinear points are also coplanar, but not all coplanar points are collinear. For instance, four points on a plane can be coplanar without forming a straight line.

In summary, collinear points share the same line, and coplanar points share the same plane. These terms help us describe the relationships between points in space.

Notating Points

In geometry, we use capital letters to name and notate points. A point represents an exact location in space. It doesn’t have any size, shape, or dimension. For example, if there’s a point on a line, you might call it Point A. If there are more points, you could name them Point B, Point C, and so on.

When writing about points, you use a single capital letter. For example, if you’re describing a point on a diagram, you might write it as Point P. Sometimes, in diagrams, points are shown as dots with their names written next to them.

Notating points helps us label and keep track of specific locations in diagrams or problems. It’s especially useful when working with shapes, lines, or angles. For instance, if a triangle has three corners, you might name them Point A, Point B, and Point C to make it easier to refer to each corner.

In summary, points are named with capital letters, and this simple way of notating them helps us communicate clearly in geometry.