Surface Area

What is Surface Area?

The surface area in geometry is the total area of all the faces or curved surfaces of a three-dimensional object. For example, the surface area of a sphere is calculated as $4\pi r^2$ , where $r$ is the radius.

Examples

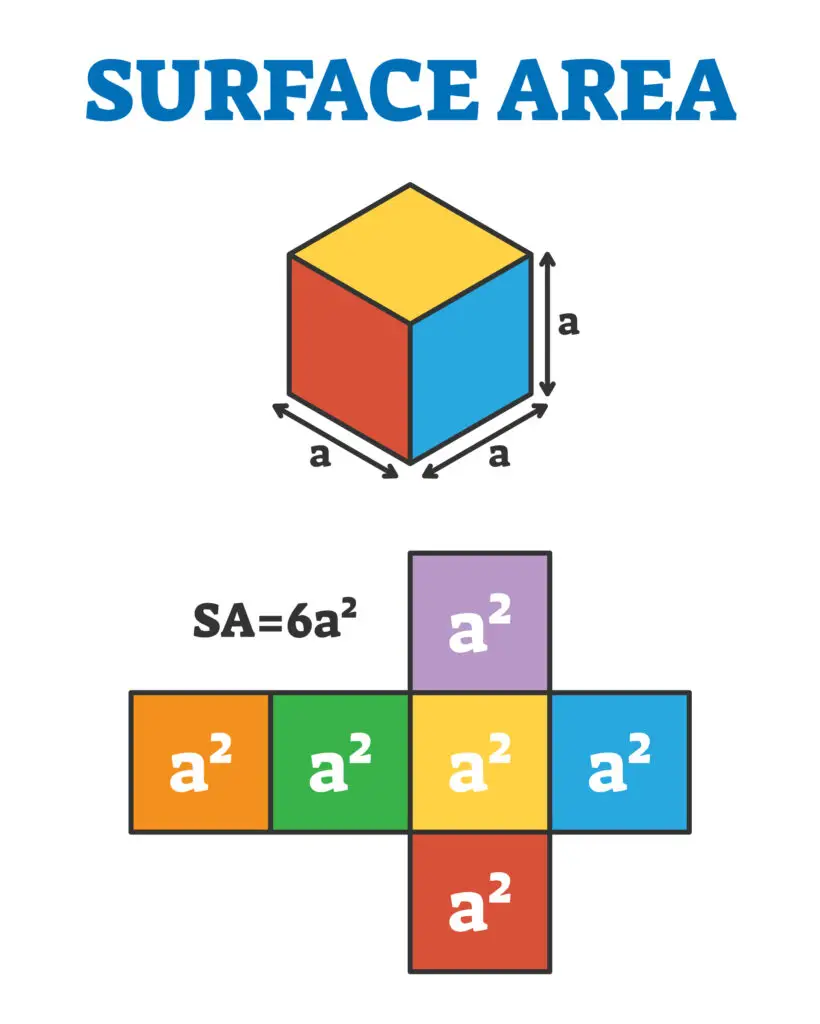
1. Surface Area of a Cube

Problem:

A cube has sides that are each 5 cm long. Find its surface area.

Step-by-Step Solution:

Understand the Formula:
The formula for the surface area of a cube is:
$\text{Surface Area} = 6 \times \text{side}^2$
Plug in the Side Length:
Since the side length of the cube is 5 cm, substitute $\text{side} = 5$ into the formula:
$\text{Surface Area} = 6 \times 5^2$
Calculate the Square of the Side:
$5^2 = 25$
Multiply by 6:
$6 \times 25 = 150$
Include the Unit:
The surface area is $150 \text{ cm}^2$ .

Final Answer:

The surface area of the cube is $150 \text{ cm}^2$ .

2. Surface Area of a Rectangular Prism (or Box)

Problem:

A rectangular prism has a length of $8 \text{ cm}$ , a width of $5 \text{ cm}$ , and a height of $3 \text{ cm}$ . Find its surface area.

Step-by-Step Solution:

Understand the Formula: The formula for the surface area of a rectangular prism is: $\text{Surface Area} = 2lw + 2lh + 2wh$ where $l$ is the length, $w$ is the width, and $h$ is the height.
Plug in the Dimensions: Substitute $l = 8$ , $w = 5$ , and $h = 3$ into the formula: $\text{Surface Area} = 2(8 \times 5) + 2(8 \times 3) + 2(5 \times 3)$
Calculate Each Term:
- First term: $2(8 \times 5) = 2(40) = 80$
- Second term: $2(8 \times 3) = 2(24) = 48$
- Third term: $2(5 \times 3) = 2(15) = 30$
Add the Results: $\text{Surface Area} = 80 + 48 + 30 = 158$
Include the Unit: The surface area is $158 \text{ cm}^2$ .

Final Answer:

The surface area of the rectangular prism is $158 \text{ cm}^2$ .